Terzaghi's One-Dimensional Consolidation Theory
Assumptions
- Loading is one-dimensional. Settlement and flow of water is vertical.
- Compressibility is constant
- Permeability is constant
- Flow is controlled by Darcy's law
- Secondary compression does not occur
- Deformations are small, such that strains may be computed from undeformed geometry
- Soil is saturated and uniform
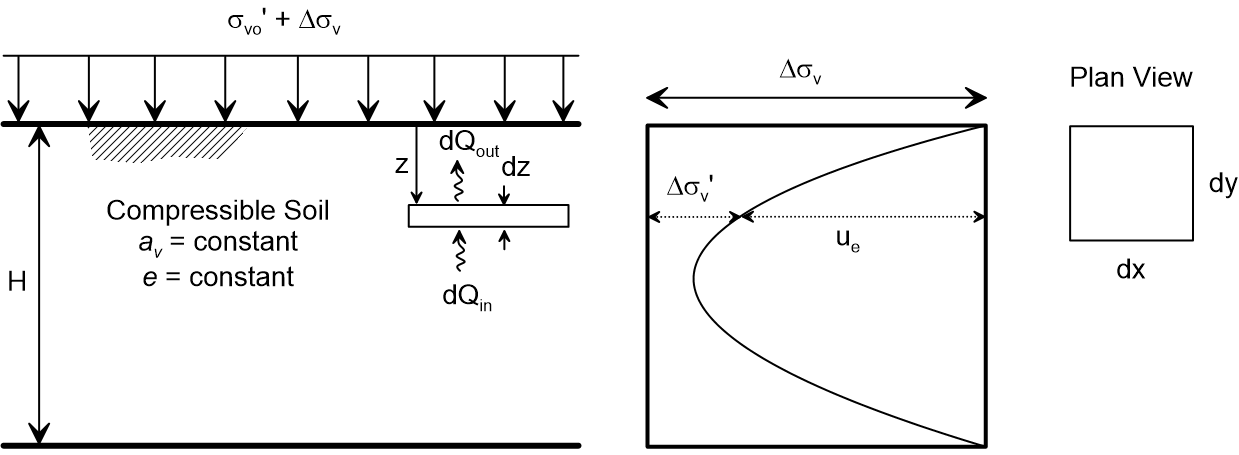
Volume Change Based on Flow
Darcy's law:
\(\qquad\frac{dQ}{dt} = k i A = k i dx dy\);
Flow out of element:
\(\qquad dQ_{out} = k i_z dx dy dt\)
Hydraulic gradient at depth z:
\(\qquad i_z = \frac{1}{\gamma_w}\frac{\partial u_e}{\partial z}\)
Flow into element:
\(\qquad dQ_{in} = k i_{z+dz} dx dy dt\)
Hydraulic gradient at depth z + dz:
\(\qquad i_{z+dz} = i_z + \frac{\partial i_z}{\partial z}dz\)
\(\qquad i_{z+dz} = \frac{1}{\gamma_w}\frac{\partial u_e}{\partial z} + \frac{1}{\gamma_w}\frac{\partial^2 u_e}{\partial z^2}dz \)
Change in flow:
\(\qquad dQ = dQ_{out} - dQ_{in}\) (Compression positive)
\(\qquad dQ = -\frac{k}{\gamma_w}\frac{\partial^2 u_e}{\partial z^2}dx dy dz dt\)
Assuming volume change is due entirely to flow of water out of the element:
\(\qquad dV = dQ\)
\(\qquad dV = -\frac{k}{\gamma_w}\frac{\partial^2 u_e}{\partial z^2}dx dy dz dt\)
\(\qquad\frac{dQ}{dt} = k i A = k i dx dy\);
Flow out of element:
\(\qquad dQ_{out} = k i_z dx dy dt\)
Hydraulic gradient at depth z:
\(\qquad i_z = \frac{1}{\gamma_w}\frac{\partial u_e}{\partial z}\)
Flow into element:
\(\qquad dQ_{in} = k i_{z+dz} dx dy dt\)
Hydraulic gradient at depth z + dz:
\(\qquad i_{z+dz} = i_z + \frac{\partial i_z}{\partial z}dz\)
\(\qquad i_{z+dz} = \frac{1}{\gamma_w}\frac{\partial u_e}{\partial z} + \frac{1}{\gamma_w}\frac{\partial^2 u_e}{\partial z^2}dz \)
Change in flow:
\(\qquad dQ = dQ_{out} - dQ_{in}\) (Compression positive)
\(\qquad dQ = -\frac{k}{\gamma_w}\frac{\partial^2 u_e}{\partial z^2}dx dy dz dt\)
Assuming volume change is due entirely to flow of water out of the element:
\(\qquad dV = dQ\)
\(\qquad dV = -\frac{k}{\gamma_w}\frac{\partial^2 u_e}{\partial z^2}dx dy dz dt\)
Volume Change Based on Phase Relations
Volumetric strain:
\(\qquad\epsilon_v = -\frac{de}{1+e}\) (Compression positive)
Compressibility:
\(\qquad a_v = -\frac{de}{d\sigma_v}\); (Compression positive)
\(\qquad de = -a_v d\sigma_v\)
Change in effective stress is equal to negative of change in pore pressure:
\(\qquad d\sigma_v = -du_e\);
\(\qquad de = a_v du_e\)
Partial derivative expression for \(du_e\):
\(\qquad du_e = \frac{\partial u_e}{\partial t}dt\)
Substituting into volumetric strain:
\(\qquad\epsilon_v = -\frac{a_v}{1+e}\frac{\partial u_e}{\partial t}dt\)
Volume change:
\(\qquad dV = \epsilon_v dx dy dz\)
\(\qquad dV = -\frac{a_v}{1+e}\frac{\partial u_e}{\partial t}dt dx dy dz\)
\(\qquad\epsilon_v = -\frac{de}{1+e}\) (Compression positive)
Compressibility:
\(\qquad a_v = -\frac{de}{d\sigma_v}\); (Compression positive)
\(\qquad de = -a_v d\sigma_v\)
Change in effective stress is equal to negative of change in pore pressure:
\(\qquad d\sigma_v = -du_e\);
\(\qquad de = a_v du_e\)
Partial derivative expression for \(du_e\):
\(\qquad du_e = \frac{\partial u_e}{\partial t}dt\)
Substituting into volumetric strain:
\(\qquad\epsilon_v = -\frac{a_v}{1+e}\frac{\partial u_e}{\partial t}dt\)
Volume change:
\(\qquad dV = \epsilon_v dx dy dz\)
\(\qquad dV = -\frac{a_v}{1+e}\frac{\partial u_e}{\partial t}dt dx dy dz\)
Equate Volume Change Expressions
\(\qquad -\frac{k}{\gamma_w}\frac{\partial^2 u_e}{\partial z^2}dx dy dz dt = -\frac{a_v}{1+e}\frac{\partial u_e}{\partial t}dt dx dy dz\)
Collect terms:
\(\qquad\frac{k}{\gamma_w}\frac{1+e}{a_v}\frac{\partial^2 u_e}{\partial z^2} = \frac{\partial u_e}{\partial t}\)
Define coefficient of consolidation, \(c_v\):
\(\qquad c_v = \frac{k}{\gamma_w}\frac{1+e}{a_v}\)
Terzaghi's one-dimensional consolidation equation:
\(\qquad c_v\frac{\partial^2 u_e}{\partial z^2} = \frac{\partial u_e}{\partial t}\)
Commonly the subscript "e" is dropped from the "u" term, based on the implicit assumption we are talking about excess pore pressures here:
\(\qquad c_v\frac{\partial^2 u}{\partial z^2} = \frac{\partial u}{\partial t}\)
Collect terms:
\(\qquad\frac{k}{\gamma_w}\frac{1+e}{a_v}\frac{\partial^2 u_e}{\partial z^2} = \frac{\partial u_e}{\partial t}\)
Define coefficient of consolidation, \(c_v\):
\(\qquad c_v = \frac{k}{\gamma_w}\frac{1+e}{a_v}\)
Terzaghi's one-dimensional consolidation equation:
\(\qquad c_v\frac{\partial^2 u_e}{\partial z^2} = \frac{\partial u_e}{\partial t}\)
Commonly the subscript "e" is dropped from the "u" term, based on the implicit assumption we are talking about excess pore pressures here:
\(\qquad c_v\frac{\partial^2 u}{\partial z^2} = \frac{\partial u}{\partial t}\)