4.3 Mohr Circle and the Pole Method

A graphical solution to the two-dimensional stress state on a plane inclined at any angle can be solved using the Mohr Circle. The steps are as follows:

1. Plot stress state and draw Mohr Circle

Figure 4.3.1a. Graphical solution of stresses on inclined plane: Step 1.

2. Draw line from (\(\sigma_{22},\sigma_{12}\)) in a direction perpendicular to the line of action of \(\sigma_{22}\). We assume here that \(\sigma_{22}\) acts vertically such that the line through (\(\sigma_{22},\sigma_{12}\)) is horizontal as illustrated in Figure 4.3.1b.

Figure 4.3.1b. Graphical solution of stresses on inclined plane: Step 2.

3. Draw line from (\(\sigma_{11},\sigma_{12}\)) in a direction perpendicular to the line of action of \(\sigma_{11}\).

Figure 4.3.1c. Graphical solution of stresses on inclined plane: Step 3.

4. The intersection of the lines from Step 2 and 3 is called the "pole". The pole is a unique point on the Mohr circle because the stress state along a plane inclined at any angle \(\theta\) is defined by the intersection of the Mohr circle with a line drawn from the pole at an angle \(\theta\).

Figure 4.3.1d. Graphical solution of stresses on inclined plane: Step 4.

5. Draw a line angled at \(\theta\) from horizontal and \(\theta\) from vertical. The intersection of these lines with the Mohr circle defines the state of stress.

Figure 4.3.1e. Graphical solution of stresses on inclined plane: Step 5.

You may notice that we are using \(\theta\) to define the angle when we use the pole method, while we use \(\gamma\) to define the angle when we used the rotation matrix in the previous section. There is a good reason for this. \(\theta\) is an angle measured relative to the specific coordinate system under consideration, while \(\gamma\) is a change of angle from a reference plane to a rotated plane. Say, for example, that we know the stress condition for an element on planes that lie at angles \(\theta_1\) from horizontal and vertical, and we wish to find stresses on different planes rotated at angles \(\theta_2\) from horizontal and vertical. In this case, \(\gamma\) = \(\theta_2\) - \(\theta_1\). When finding the pole, it is important to draw the lines perpendicular to the line of action \(\sigma_{22}\) and \(\sigma_{11}\) in steps 2 and 3, respectively.

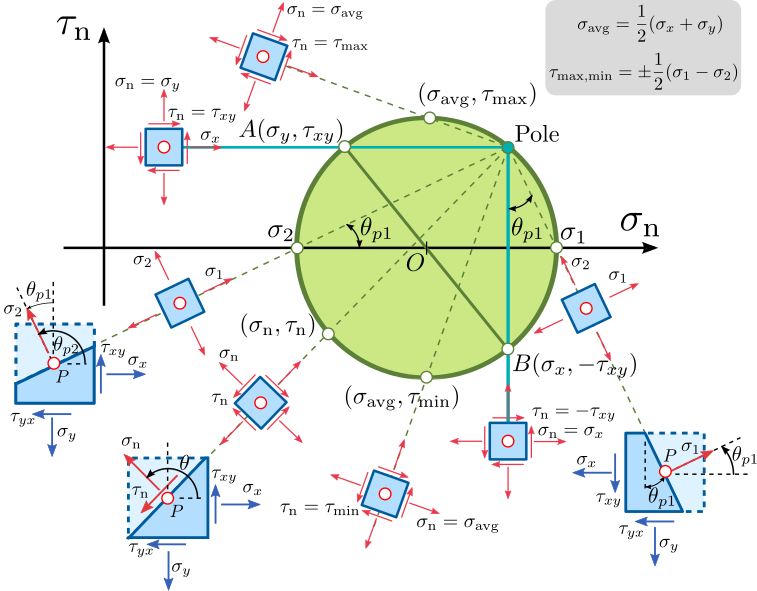
Figure 4.3.2. Mohr's circle for plane stress and plane strain conditions (Pole approach).
https://upload.wikimedia.org/wikipedia/commons/thumb/b/bd/Mohr_Circle_plane_stress_%28pole%29.svg/757px-Mohr_Circle_plane_stress_%28pole%29.svg.png